https://www.acmicpc.net/problem/26009
💡문제 분석 요약
- 출발지점이 주어지고 도착지점까지 최단 시간에 가는 방법구하기
- 이때, 장애 구간을 피해서 가야한다.
- 장애지점(Ri, Ci)과 거리(Di)가 각각 주어진다.
- → (Ri, Ci)로부터 거리가 Di 이하인 거리가 모두 장애 지점이 된다.
- 이때, 두 칸 (R1, C1), (R2, C2)사이의 거리는 |R1 − R2| + |C1 − C2|와 같다.
- 장애지점(Ri, Ci)과 거리(Di)가 각각 주어진다.
- [입력 조건]
- 첫째 줄에 격자의 크기 N, M이 주어진다. (2 ≤ N, M ≤ 3,000)
- 다음 줄에 정체 구역의 수 K가 주어진다. (1 ≤ K ≤ 3,000)
- 다음 K개 줄에 걸쳐 각 정체 구역의 정보 Ri, Ci, Di가 주어진다. (1 ≤ Ri ≤ N, 1 ≤ Ci ≤ M, 0 ≤ Di ≤ 3,000)
- (1, 1) 또는 (N, M)에 교통 정체가 일어나고 있는 경우는 주어지지 않는다.
💡알고리즘 설계
- 그냥 BFS처럼 보이지만 장애물이 하나의 정점에 있는 것이 아니라 “구간으로” 주어진다. << 이 부분을 주목하자!!!🥊
- 그러므로 그 구간에 대해 모든 정점을 장애물 표시하려면
- R * C * 장애물 수 ⇒ 3000 * 3000 * 3000이므로 완탐으로 하면 시간초과가 난다.ㅠㅠ
- 아래의 코드는 완탐으로 하는 코드이며 시간 초과가 난다.
public void checkEveryPoint(int y, int x, int d){ // | x1 - x2 | + | y1 - y2 | = d 를 만족하는 모든 정점 for(int i = 0 ; i < R; i++) { for(int j = 0; j < C; j++){ if(Math.abs( i - y) + Math.abs(j - x) == d){ map[i][j] = -1; } } } } - 그렇다면 어떻게 시간초과를 개선할 수 있을까? ....
- ⇒ 장애 구간에 대한 모든 점을 검사하는 대신, 맨해튼 거리에서 마름모 형태로 영역이 생기게 되므로 이에 대한 경계에 있는 점들만을 탐색한다.
- 그러므로 그 구간에 대해 모든 정점을 장애물 표시하려면
int[][] diagonal = {{-1, 1},{1, 1},{1, -1},{-1, -1}};
public void check(int y, int x, int d) {
map[y][x] = -1;
int ny = y;
int nx = x - d;
for(int i=0; i<4; i++) {
for(int j=0; j<d; j++) {
nx += diagonal[i][1];
ny += diagonal[i][0];
if(!isRange(nx, ny)) continue;
map[ny][nx] = -1;
}
}
}
✔️ 예시 설명)
- 전체 좌표가 (9, 9) 일 때, 장애지점이 (5, 5)이고, d = 3일 때 예시를 들어보자.
- 먼저 아래 코드 부분이 실행이 되면 아래의 그림과 같이 해당 영역이 표시된다.
int ny = y;
int nx = x - d;

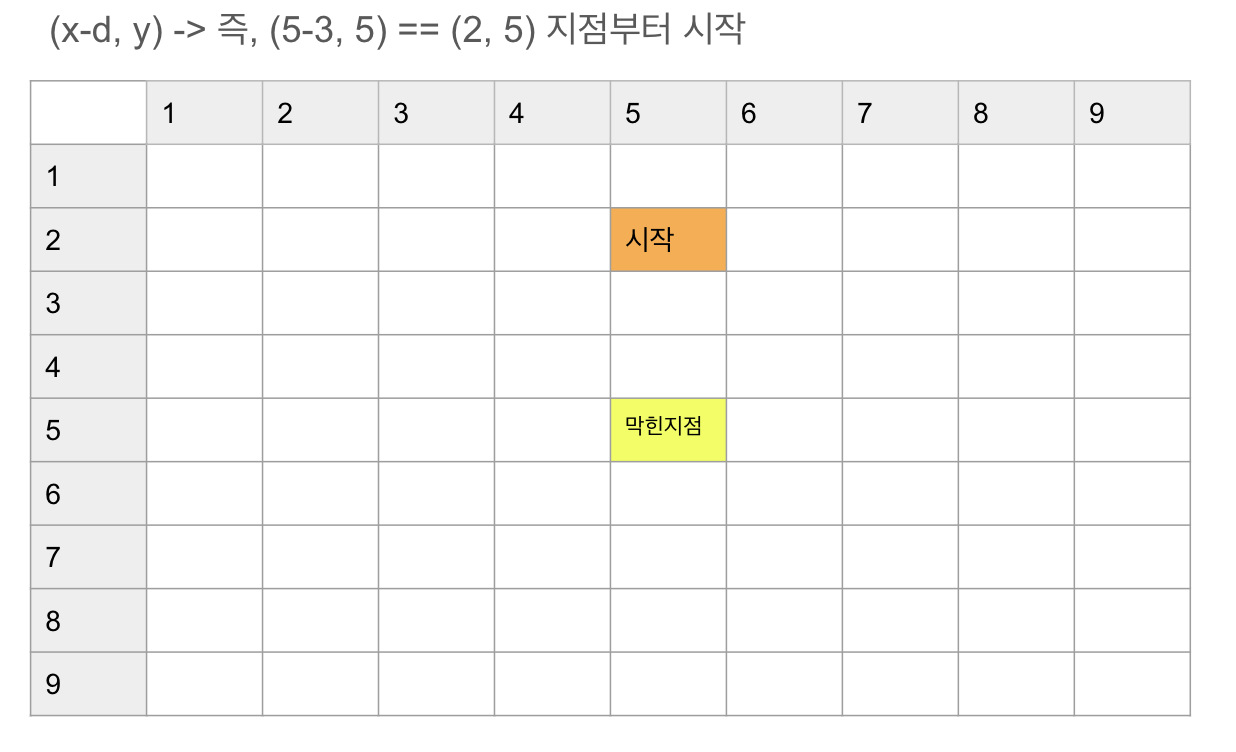
- 그 다음 2중 for문을 실행하는데 밖에 있는 for문은 4개의 방향을 나타내며, d는 거리만큼 그 방향으로 가는 것을 의미한다.
- 예시에서는 d=3이므로 각 방향마다 3번 반복하며 경계선을 표시한다.
for(int i=0; i<4; i++) { //diagonal 배열을 사용하여 네 방향 각각을 처리
for(int j=0; j<d; j++) { //각 방향에서 d번 만큼 점을 이동
nx += diagonal[i][1];
ny += diagonal[i][0];
if(!isRange(nx, ny)) continue;
map[ny][nx] = -1;
System.out.println(ny + " " + nx);
}
}



2번째 방향


이런식으로 계속 반복하면 ... 결국!!!! 짜잔~


이렇게 마름모 형태로 경계선만 표시할 수 있게 된다!
그리고 bfs를 진행해주면 장애 영역을 피해서 목적지에 도착할 수 있는 최단 시간을 구할 수 있다.
💡코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.*;
public class 험난한등굣길 {
// 최소 이동 횟수 구하기
public static void main(String[] args) throws Exception{
new 험난한등굣길().solution();
}
int R;
int C;
int areaNum;
int[][] map;
public void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
R = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
areaNum = Integer.parseInt(br.readLine());
map = new int[R][C];
for(int i = 0; i < areaNum; i++){
st = new StringTokenizer(br.readLine());
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
checkEveryPoint(r-1, c-1, a); // 장애물 있는 부분의 모서리 부분을 체크해둠
}
bfs();
}
static int[] dx = new int[]{0, 0, -1, 1};
static int[] dy = new int[]{-1, 1, 0, 0};
int[][] diagonal = {{-1, 1},{1, 1},{1, -1},{-1, -1}}; //사각형의 네 모서리로, 각 모서리에서 다음 모서리로 이동할 때 사용
public void check(int y, int x, int d) {
map[y][x] = -1;
int ny = y;
int nx = x - d;
for(int i=0; i<4; i++) { //diagonal 배열을 사용하여 네 방향 각각을 처리
for(int j=0; j<d; j++) { //각 방향에서 d번 만큼 점을 이동
nx += diagonal[i][1];
ny += diagonal[i][0];
if(!isRange(nx, ny)) continue;
map[ny][nx] = -1;
System.out.println(ny + " " + nx);
}
}
}
public void bfs(){
Deque<Node> que = new ArrayDeque<>();
boolean visited[][] = new boolean[R][C];
que.offer(new Node(0, 0, 0));
visited[0][0] = true;
while(!que.isEmpty()){
Node cur = que.poll();
if(cur.x == C-1 && cur.y == R-1){
System.out.println("YES");
System.out.println(cur.cnt);
return;
}
for(int i = 0; i < 4; i++){
int nx = dx[i] + cur.x;
int ny = dy[i] + cur.y;
if(isRange(nx, ny) && map[ny][nx] != -1 && !visited[ny][nx]){
que.offer(new Node(nx, ny, cur.cnt+1));
visited[ny][nx] = true;
}
}
}
System.out.println("NO");
}
public boolean isRange(int x, int y){
if(x >= 0 && y >= 0 && x < C && y < R){
return true;
}
return false;
}
class Node{
int x;
int y;
int cnt;
public Node(int x, int y, int cnt){
this.x = x;
this.y = y;
this.cnt = cnt;
}
}
}
'CS > 알고리즘' 카테고리의 다른 글
| [백준] 가희와 은행 22234 (라운드로빈) (0) | 2024.06.12 |
|---|---|
| [스택] Monotonic Stack (2) | 2024.04.22 |
| [백준] 1158 요세푸스 (1) | 2024.03.05 |
| [알고리즘] stack 문제 비교 (백준 - 2493, 17298, 6198) (2) | 2023.10.16 |
| [백준] 25418 정수 a를 k로 만들기 (0) | 2023.08.13 |




