연속 행렬 곱셈(Chained Matrix Multiplication)
문제 = 연속된 행렬들의 곱셈에 필요한 원소 간의 최소 곱셈 횟수를 찾는 문제
행렬 곱셈
(1) 두 행렬의 곱셈이란?
두 행렬 A, B가 있다.
A = 10 x 20
B = 20 x 5 라면
총 곱셈의 횟수 = 10 * 20 * 5 = 1000이다.
(2) 3개의 행렬 곱셈
A = 10 x 20
B = 20 x 5
C = 5 x 15
행렬의 곱셈은 결합법칙 성립하므로 (A* B) * C , A * ( B * C) 이 둘 다 성립한다.
하지만 둘의 결과값는 같지만 곱셈의 횟수는 전자가 더 적다.(과정이 다르다)
[ 행렬 곱셈의 주의점 ]
주어진 행렬의 순서를 지켜서 “반드시 이웃하는 행렬끼리” 곱해야 한다.
동적 알고리즘 적용
(1) 부분 문제
행렬 A, B, C, D, E가 있다. 이 행렬들을 곱하려고 할 때의 경우들을 생각해볼 수 있다.
단, 행렬의 곱셈의 특성 상 이웃하는 행렬끼리만 곱한다는 것을 고려하여 나올 수 있는 경우들을 생각한 것이다.

알고리즘
C[i, j] = 최소 곱셈 횟수 저장 공간
입력: 연속된 행렬 A1xA2x⋯xAn , 단, A1은 d0xd1, A2는 d1xd2 , ⋯, An은 dn-1xdn이다.
출력: 입력의 행렬 곱셈에 필요한 원소의 최소 곱셈 횟수
1. for i = 1 to n
2. C[i, i] = 0 //자기 자신은 곱할 필요 없으므로 0이다.
3. for L = 1 to n-1 // L은 부분 문제의 크기를 조절하는 인덱스이다.
4. for i = 1 to n-L //부분 문제는 1개씩 줄어든다. (앞의 표에서 부분 문제의 개수 5, 4, 3, 2, 1 순으로 줄어드는 것을 표현)
5. j = i + L
6. C[i, j] = ∞ //일단 이렇게 두자
7. for k = i to j-1
8. temp = C[i, k] + C[k+1, j] + di-1dkdj //
9. if (temp < C[i, j])
10. C[i, j] = temp
11. return C[1,n]
예시를 통해 다음과 같은 과정을 이해해보자.
4개의 행렬을 곱하는 문제가 있다고 하자
그렇다면 L(부분 문제의 크기)는 1, 2, 3, 4개가 가능할 것이다.
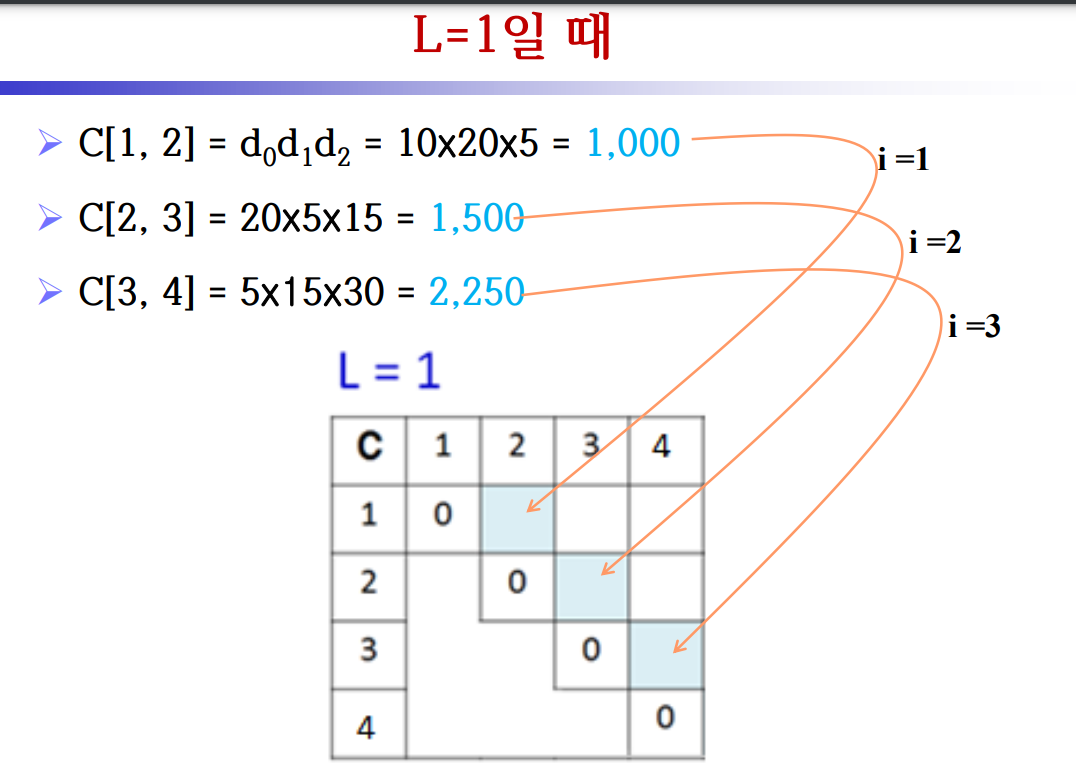
(1) L = 1일 때, i = 1 ~ 3, j = 2 ~ 4
- i = 1일 때 , k = 1
temp = C[1, 1] + C[2, 2] + 10 * 20 * 5 = 1000
- i = 2일 때 , k = 2
temp = C[2, 2] + C[3, 3] + 20 * 5 * 15 = 1500
- i = 3일 때, k = 2
temp = C[3, 3] + C[4, 4] + 5 * 15 * 30 = 2250

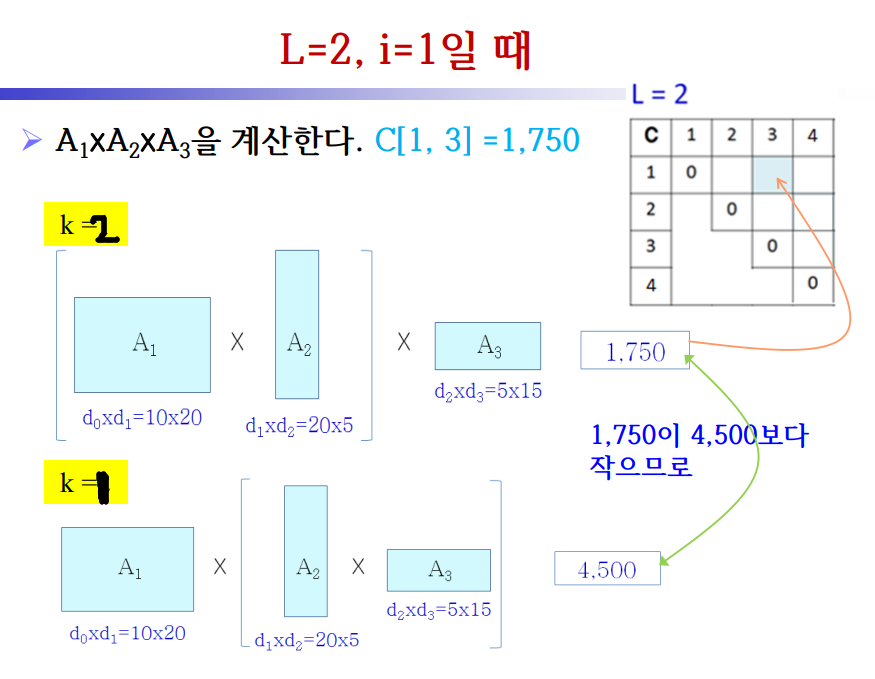
(2) L = 2 일 때, i = 1~2 , j = 3 ~4
[ i = 1 ]
1) k = 1일 때
[i = 1, j = 3, k = 1]
temp = C[1, 1] + C[2, 3] + 10 * 20 * 15 = 4500
*C[2, 3]이라는 의미는 A2와 A3을 먼저 곱하고 A1을 곱한다는 것이다.
*10 * 20 * 15은 새로 추가된 부분의 곱셈 횟수
ex) A = a*b 행렬이 있고 B = c * d행렬이 있다고 하자 곱셈을 하는 횟수는 a * c * d이다.
2) k = 2일 때
temp = C[1, 2]+ C[3, 3] + 10 * 5 * 15 = 1750
[ i = 2 ]
i = 2, j = 4 → A2 ~ A4의 행렬을 곱하라
(1) k = 2
temp = C[2, 2] + C[3, 4] +20 * 5 * 30 = 5250
A3, A4를 먼저 곱하고 A2를 곱하는 방법이라고 할 수 있다.
(2) k = 3
temp = C[2, 3] + C[4, 4] + 20 * 15 * 30 = 5250

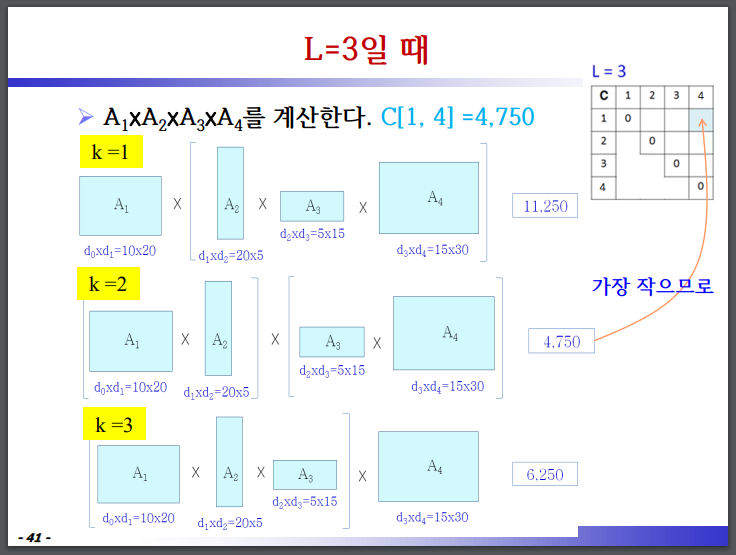
(3) L = 3, i = 1, j = 4
A1 ~ A4 까지 행렬이 곱을 구하자
- k = 1
temp = C[1, 1] + C[2, 4] + 10 * 20 * 30 = 11250
- k = 2
temp = C[1, 2] + C[3, 4] + 10 * 5 * 30 = 4750
- k = 3
temp = C[1, 3] + C[4, 4] + 10 * 15 * 30 = 620
[코드 구현]
#include <stdio.h>
#include <stdlib.h>
#define INF 10000000
#define N 5
void print(int C[N][N])
{
printf("======");
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
printf("%4d", C[i][j]);
}
printf("\\n");
}
}
void matrinxChain(int C[N][N], int D[n])
{
for(int L = 1 ; L < N-1 ; L++){
for(int i = 1; i < N-L; i++)
{
int j = i + L; //L, i, j 세팅
C[i][j] = INF;
for (int k = i; k < j ; k++)
{
int temp = C[i][k] + C[k+1][j] + D[i-1] * D[j];
if(temp < C[i][j])
{
C[i][j] = temp;
}
}
}
printf("\\nL == %d\\n", L);
print(C);
}
}
int main()
{
int D[N] = {10, 20, 5, 15, 30};
int C[N][N] = {0}; //0으로 초기화
matrixChain(C, D);
return 0;
}
시간 복잡도
O(n^3)
'CS > 알고리즘' 카테고리의 다른 글
| Chap 6. 정렬 알고리즘(sort) (0) | 2022.05.28 |
|---|---|
| Chap 5-3. 편집거리 (Edit Distance) (0) | 2022.05.27 |
| Chap 5-1. 0-1 배낭 문제 (0) | 2022.05.06 |
| Chap 5. 동적 계획 알고리즘 (0) | 2022.05.05 |
| Chap 4-7. 허프만 압축 (0) | 2022.05.04 |




