3.4 최근접 점의 쌍 찾기
= 최근접 점의 쌍(closest pair)문제는 2차원 평면 상의 n개의 점이 입력으로 주어질 때,
거리가 가장 가까운 한 쌍의 점을 찾는 문제이다.
ex) 기상 예보, 외판원 문제 등에서 사용
[가장 간단한 방법 구현]
모든 점에 대해서 각각의 두 점 사이의 거리를 계산하여 가장 가까운 점을 찾는 방법
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define N 10
typedef struct
{
int x, y;
}Point;
void print(Point p[]) {
for (int i = 0; i < N; i++)
printf("[%d %d]", p[i].x, p[i].y);
printf("\\n");
}
double dist(Point p1, Point p2)
{
return sqrt(pow((p1.x - p2.x), 2) + pow((p1.y - p2.y), 2));
}
double insertSortX(Point p[]) { //일단 x를 정렬한다. 알고리즘은 상관없다. y도 정렬해주면 좋다-> 복잡도 줄어든다.
int i, j, key;
for (i = 1; i < N; i++)
{
Point t = p[i];
key = p[i].x;
for (j = i - 1; j >= 0 && p[j].x > key; j--)
{
p[j + 1] = p[j];
}
p[j + 1] = t;
}
}
void closestPairIter(Point p[])
{
double dMin = 10000000.0, d; // 최솟값에 일단 최대 숫자 넣기
int iMin, jMin;// 최소 점의 index(두 점의 인덱스)
for (int i = 0; i > N - 1; i++)
{
for (int i = 0; i < N - 1; i++) // 0부터 돌면서
{
for (int j = i + 1; j < N; j++) { // i+1부터 확인한다.
d = dist(p[i], p[j]);
if (d < dMin) {
dMin = d;
iMin = i;
jMin = j;
}
}
}
}
printf("[%d %d] [%d %d] %.2f\\n", p[iMin].x, p[iMin].y, p[jMin].x, p[jMin].y, dMin);
}
int main()
{
Point p[N];
srand(time(NULL));
for (int i = 0; i < N; i++)
{
p[i].x = rand() % 100;
p[i].y = rand() % 50;
}
printf(p);
closestPairIter(p);
return 0;
}
[시간 복잡도]
n개 중 2개의 조합으로 만드는 경우의 수 = n(n-1) ⇒ O(n^2)
한 쌍의 거리 계산 = O(1)
따라서, O(n^2) * O(1) = O(n^2)
❤효율적인 방법
= O(n^2)보다 효율적인 분할 정복 이용
(1) n개의 점을 1/2로 분할하여 < 계속 반으로 분할>
(2) 각각의 부분 문제에서 최근접 점의 쌍을 찾고,
(3) 2개의 부분 해 중에서 짧은 거리를 가진 점의 쌍을 일단 찾는다.
**주의 = 반으로 나눈 왼쪽 부분과 오른쪽 부분끼리에서만 최단 거리의 점들의 쌍을 찾았는데 왼쪽과 오른쪽의 경계가 있는 중간 영역도 고려를 해야 한다.
중간 영역 안의 점들
만약 왼쪽 오른쪽 영역에서 최단 거리가 10이라면 중간 경계로부터 왼쪽방향으로 방향으로 10만큼의 영역을 만들고, 오른쪽도 중간 경계로부터 오른쪽 방향으로 10만큼 영역을 확보한다.
이유 = 최단 거리가 일단 최단 거리가 10이므로 이보다 작아야 한다.
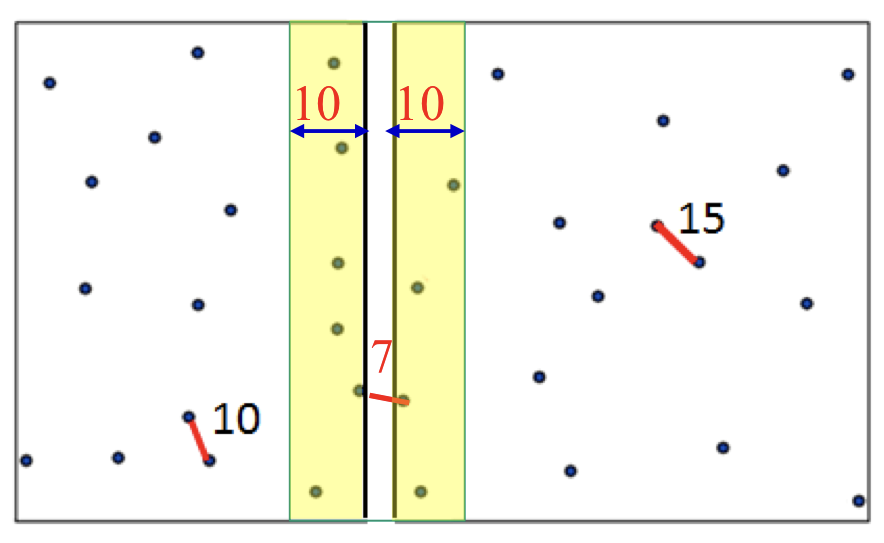
[ 중간 영역에 있는 점들을 찾는 방법 ]
d = min { 왼쪽 부분의 최근접 점의 쌍 사이의 거리, 오른쪽 부분의 최근접 점의 쌍 사이의 거리 }
(2) x좌표 기준으로 오름차순으로 나열하면 나열한 중간부분이 왼쪽 부분과 오른쪽 부분의 “중간 영역”이라고 할 수 있다.
(3) 중간 영역의 속한 점 = “(왼쪽 부분에서 중간 영역에 가장 가까운 점) - d”보다 큰 값들과
“(오른쪽 부분에서 중간 영역에 가장 가까운 점) - d”보다 작은 값들이다.
[의사코드]
ClosestPair(S)
입력: x-좌표의 오름차순으로 정렬된 배열 S에 있는 i개의 점. 단, 각 점은 (x,y)로 표현
출력: S에 있는 점들 중 최근접 점의 쌍의 거리
1. if (i ≤ 3) return (2 또는 3개의 점들 사이의 최근접 쌍) // 분할된 영역 안에 점의 수가 3개 이하이면 더 이상 분할 필요가 없음
2. 정렬된 S를 같은 크기의 SL과 SR로 분할한다. |S|가 홀수이면, |SL| = |SR|+1이 되도록 분할
3. CPL = ClosestPair(SL) // CPL은 SL에서의 최근접 점의 쌍
4. CPR = ClosestPair(SR) // CPR은 SR에서의 최근접 점의 쌍
5. d = min{dist(CPL), dist(CPR)}일 때, 중간 영역에 속하는 점들 중
에서 최근접 점의 쌍을 찾아서 이를 CPC라고 하자. 단, dist()는 두 점 사이의 거리
6. return (CPL, CPC, CPR 중에서 거리가 가장 짧은 쌍)
if( n==2)
return (두 점사이의 거리)
else if(n == 3)
return min(a, b, c) // 점 3개 중의 min값을 리턴
else
mid = (left + right ) /2 //배열의 정중앙값
d1 = CP(x ≤ mid) // 왼쪽 부분
d2 = CP(x > mid) // 오른쪽 부분
d = min(d1, d2) // d1과 d2의 거리 (최근접 점의 쌍의 거리)
d3 = mid - d < x < mid + d //영역에 있는 점들을 처리한다. 여기서 d3를 찾는다.
return (d, d3); //cpl cpr중에 하나와 d3(중간 영역)
[중간 영역을 고려하여 최솟값을 찾는 방법 -코드 구현 ]
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define N 10;
typedef struct
{
int x, y;
}Point;
void print(Point p[]) {
for (int i = 0; i < N; i++)
printf("[%d %d]", p[i].x, p[i].y);
printf("\\n");
}
double dist(Point p1, Point p2)
{
return sqrt(pow((p1.x - p2.x), 2) + pow((p1.y - p2.y), 2));
}
double insertSortX(Point p[]) { //일단 x를 정렬한다. 알고리즘은 상관없다. y도 정렬해주면 좋다-> 복잡도 줄어든다.
int i, j, key;
for (i = 1; i < N; i++)
{
Point t = p[i];
key = p[i].x;
for (j = i - 1; j >= 0 && p[j].x > key; j--)
{
p[j + 1] = p[j];
}
p[j + 1] = t;
}
}
void closestPairIter(Point p[])
{
double dMin = 10000000.0, d; // 최솟값에 일단 최대 숫자 넣기
int iMin, jMin;// 최소 점의 index(두 점의 인덱스)
for (int i = 0; i > N - 1; i++)
{
for (int i = 0; i < N - 1; i++) // 0부터 돌면서
{
for (int j = i + 1; j < N; j++)
{ // i+1부터 확인한다.
d = dist(p[i], p[j]);
if (d < dMin)
{
dMin = d;
iMin = i;
jMin = j;
}
}
}
}
printf("[%d %d] [%d %d] %.2f\\n", p[iMin].x, p[iMin].y, p[jMin].x, p[jMin].y, dMin);
}
double closestPairRecur(Point p[], int left, int right)
{
int size = right - left + 1; //개수
double min;
if (size == 2) // 점이 2개라면
return dist(p[left], p[right]);
else if (size == 3) //점이 3개라면
{
double a = dist(p[left], p[left + 1]);
double b = dist(p[left + 1], p[left + 2]);
double c = dist(p[left + 2], p[left]);
if (a < b)
{
if (a < c)
return c;
}
else
{
if (b < c)
return b;
return c;
}
}
else { //분할을 해야 하는 상황이라면
int mid = (left + right) / 2;
double a = closestPairRecur(p, left, mid);
double b = closestPairRecur(p, mid + 1, right);
min = (a < b) ? a : b;
return DMZcheck(p, left, right,min ); // 중간 영역과 오른쪽-왼쪽 영역에서 찾은 최솟값과 비교
}
}
double DMZCheck(Point p[], int left, int right, double d) {
insertionSortY(p); //y-좌표를 기준으로 정렬한다. O(nlogn)이 걸린다
for (int i = left; i < right; i++)
{
for (int j = i + 1; j <= right; ++j)
{
if (p[j].y - p[i].y > d)
break;
double tmp = dist(p[i], p[j]);
d = d < tmp ? d : tmp;
}
}
return d;
}
int main()
{
Point p[N];
srand(time(NULL));
for (int i = 0; i < N; i++)
{
p[i].x = rand() % 100;
p[i].y = rand() % 50;
}
insertionSortX(p);
print(p);
closestPairIter(p);
printf("%.2f\\n", closestPairRecur(p, 0, N - 1));
return 0;
}
시간 복잡도
S 에 n 개 의 점 이 있으면 전 처 리 (preprocessing) 과정으로서 S의 점을 x-좌표로 정렬: O(nlogn)
→ 이를 코드 상에서 insertSort로 해결함 → 신경쓰지 않아도 된다< 미리 정렬하면 시간복잡도에 들어가지 않는다. 하지만 코드 중간 중간에 정렬을 하면 시간 복잡도에 들어간다.>
Line 1 [ if (i ≤ 3) return (2 또는 3개의 점들 사이의 최근접 쌍) ]
S에 3개의 점이 있는 경우에 3번의 거리 계산이 필요하고, S의 점의 수가 2이면 1번의 거리 계산이 필요하므로 O(1) 시간이 걸린다. < 상수>
Line 2 [ SL과 SR로 분할 ]
정렬된 S를 SL과 SR로 분할하는데, 이미 배열에 정렬되어 있으므로, 배열의 중간 인덱스(mid index)로 분할하면 된다. 이는 O(1) 시간 걸린다.
Line 3~4 [ CPL = ClosestPair(SL), CPL = ClosestPair(SR) ]
SL 과 SR 에 대하여 각 각 ClosestPair 를 호출하는데, 분할하며 호출되는 과정은 합병 정렬과 동일 , 시간 복잡도 = O(1) → 신경 X
Line 5 [ d = min{dist(CPL), dist(CPR)} ]
왼쪽과 오른쪽 영역으로 나눈 것들 중에서 최근접점을 찾은 상태에서 중간 영역에 속하는 점들 중에서 최근접 점의 쌍을 찾아야 한다.

(1) 이를 위해 먼저 중간 영역에 있는 점들을 y-좌표 기준으로 정렬한 후
(중간 영역에 있는 점들을 모두 계산하기보다 y좌표 기준으로 정렬한다)
(2) 아래에서 위로 각 점을 기준으로 거리가 d이내인 주변의 점들 사이의 거리를 각각 계산하며 이 영역에 속한 점들 중에서 최근접 점의 쌍을 찾는다.
- y-좌표로 정렬하는데 O(nlogn) 시간이 걸리고,
- 아래에서 위로 올라가며 각 점에서 주변의 점들 사이의 거리를 계산하는데 O(1) 시간이 걸린다.
→ 왜냐하면 각 점과 거리 계산해야 하는 주변 점들의 수는 O(1)개이기 때문
Line 6 : [return (CPL, CPC, CPR 중에서 거리가 가장 짧은 쌍) ]
3개의 점의 쌍 중에 가장 짧은 거리를 가진 점의 쌍을 리턴 → O(1)시간이 걸린다.
→ closestPair 알고리즘의 분할과정 = 합병정렬의 분할과정과 동일
그러나, closestPair 알고리즘에서는 해를 취합하여 올라가는 과정인 line 5 ~ 6에서 O(nlogn) 시간이 필요
→ k층까지 분할한 후, 층별로 line 5~6이 수행되는 (취합) 과정을 보여준다.
- 각 층의 수행 시간 O(nlogn) < 합병과정에서 원래 O(n)이지만 정렬 과정(y-좌표 기준으로 정렬) 이 있었기 때문에 O(nlogn) 인 것이다>
- 여기에 층 수인 log n을 곱하면 O(nlogn) * log n = O(nlog제곱n)
↔ 합병 과정은 O(n)만큼 걸리고 각 층이 log n만큼 있어서 O(nlogn)이 걸린다. ( n개 만큼 비교 + 층수)
[질문]
앞에서 전처리 부분으로 x를 기준으로 정렬을 해주었는데 여기서 y좌표 기준으로도 정렬을 하면 중간 영역 처리할 때 y-좌표 기준으로 정렬하는 부분을 없앨 수 있지 않나요?
= DMZ부분을 체크하면서 정렬하는 것이 아니라 이미 y축도 정렬되어져 있는 것을 대상으로 하면 되지 않나요?]
→ 가능하다.
가정 = x, y좌표 기준으로 전처리를 해준 상태 (중간에 정렬 과정 필요 없음)
T(n) = 2T(n/2) + O(n) , T(2) = T(3) = 1
T(n) = O(nlogn)
2T(n/2) = 2개로 나눈 영역이 2개가 있다. (분할과정)
O(n) = 원래 y-좌표 기준으로 정렬 과정이 필요해서 O(nlogn) * O(1) = O(nlogn)이 필요했는데 O(nlogn)의 정렬과정이 전처리 과정으로 넘겼기 때문에 정렬 과정을 하지 않아도 되므로 O(n)* O(1) = O(n)인 것이다.
T(n) = O(nlogn)
'CS > 알고리즘' 카테고리의 다른 글
| Chap4-1. 동전 찾기 문제 (0) | 2022.04.11 |
|---|---|
| Chap 4. 그리디 알고리즘 (0) | 2022.04.11 |
| Chap3-2 퀵정렬(QuickSort) (0) | 2022.04.05 |
| Chap3-1. 합병 정렬(MergeSort) (0) | 2022.04.04 |
| Chap 3. 분할 정복 알고리즘 (0) | 2022.04.02 |




